by Michael Cropper | Sep 10, 2022 | Developer |
I do this so infrequently, this blog post is mainly as a reminder to myself as a lot of content online around this topic isn’t quite as good as it could be. Anyhow. It’s important to remember how to easily mount a disk in a Linux environment so that it’s possible to control how and where you manage your data storage for your specific use case.
Context and Background
Firstly, understand your own infrastructure you’re working with – in depth. This specific blog post is based on a lab setup to provide guidance, not concrete solutions for production challenges.
The setup in this physical scenario is;
- Type 1 Hypervisor – XCP-ng
- HostOS HDDs/SSDs
- GuestOS HDDs/SSDs
- Virtual Machine running Ubuntu
- Default HDD/SSD Configured
And the scenario that we’re aiming to achieve is an additional disk mount against the ‘Virtual Machine running Ubuntu’. The reason being is that gives us a physically different location to store data against.
In this specific example, we have;
- RAID {X} Array for Type 1 Hypervisor HostOS
- RAID {X} Array for GuestOS Virtual Machines
- RAID {X} Array for Backups
All the above being on the same physical machine.
Partitioning and Formatting
Ensure your disks are partitioned and formatted so they are ready to be used if they are band new. Obviously don’t do this if you have data on the disk that you need. Again, this all comes down to your individual setup, but for ease, make sure your physical disks have been partitioned in the way that you require and have been formatted accordingly.
Attach the Disk to the Virtual Machine
Within XCP-ng Centre, make sure the virtual machine has the disk attached. Interestingly when you do this, this doesn’t mean that it is automatically available to be used interestingly so you can’t navigate to the new disk via the Linux command line, since that is installed on the disk where you installed Linux.
So next, we have to mount the new disk to the Linux installation on the main disk so that it can access that additional storage location.
Find Disk that can be Mounted
Firstly you need to SSH into your Linux virtual machine. To find the available disks, run the command;
fdisk -l
The fdisk utility is designed to manage partitions on hard drives which allows you to create, delete and partition disks for your specific use case. The L flag is for Listing the drives and their partitions. This command is extremely valuable to check if the disk has partitions or not. As you can see below, on the disk in question it has no partitions.
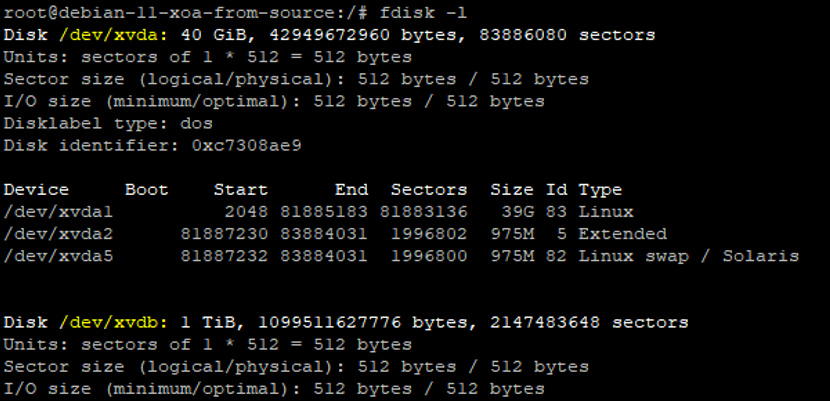
You’ll notice that the top disk in the above screenshot has a lot more information than the second disk which is showing there are no partitions on the disk. So next, we need to get those created.
Create Partition on Disk
As we can see in the previous image, the disk is at /dev/xcdb. So we need to use the fdisk command again to create a partition.
fdisk /dev/xcdb
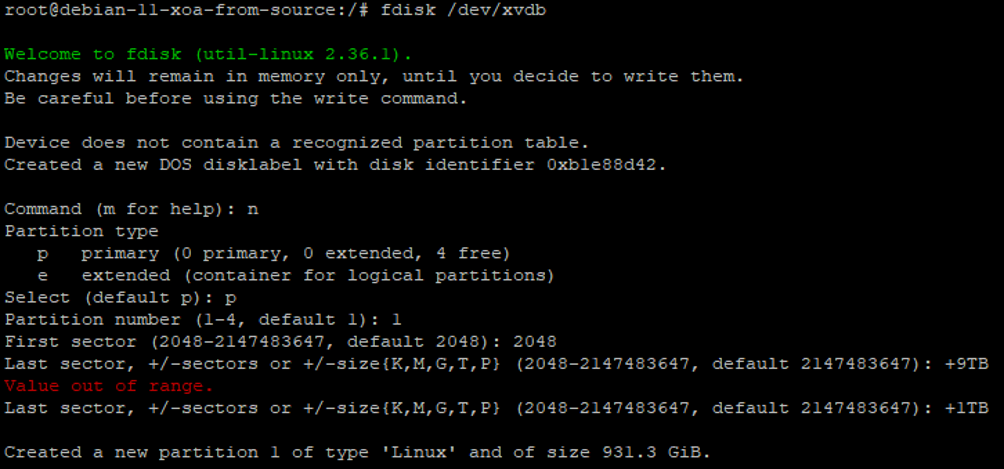
Here we can see we’ve used a couple of commands and configuration options when doing this which are primarily;
- n = New Partition
- p = Primary Partition
- 1 = Partition Number
- +1TB = Size of Partition
After following this through, we’ve now got a partition successfully created.
Next we need to write the changes to the partition table, aka. save changes, so that it is ready to be used with the w command;
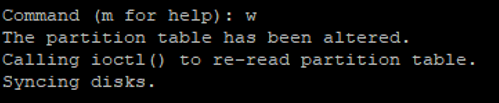
If you run the command fdisk –l again, you’ll see the partition that has been created which is setup as /dev/xvdb1.
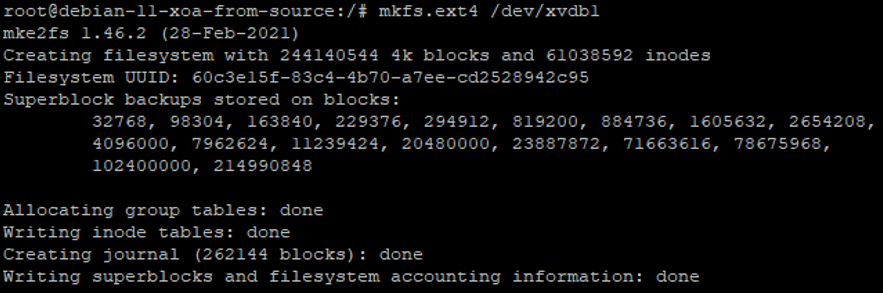
Next we need to create the file system using the command;
mkfs .ext4 /dev/xvdb1
Mount the Disk to Linux
Now we’ve got the disk partitioned and with a file system on, it’s time to mount the disk to Linux so that we can then use it. This part is straight forward now that the ground work has been done to the disk. So run the command;
mount /dev/xvdb1 /mnt/backups
Obviously change the disk name and the location folder to your specific use case.
Ensure the Mount Persists after Reboot
Finally, make sure the mount persists on reboot. To do this we use the fstab utility. To configure this, run the command nano /etc/fstab then edit the file as follows;
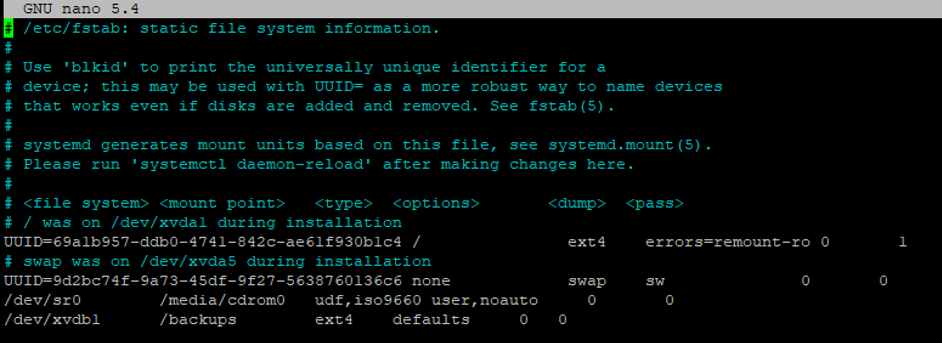
Save and exit the file. Job done. You can now use that new file system however you want as it is now accessible.
by Michael Cropper | Aug 25, 2022 | Developer |
In this blog post we’re going to look at how you can host multiple websites on separate virtual machines that sit behind a pfSense firewall with HA Proxy installed. This is quite an involved topic and one that is going to vary greatly based on your physical hardware and virtualisation environments, so keep this in mind if you’re trying to follow this.
For reference, the underlying physical hardware behind the below setup is nothing more than;
- Physical Modem
- Physical pfSense Firewall
- Physical Managed Switch
- Physical Server running XCP-ng
- Multiple Virtual Servers running inside XCP-ng
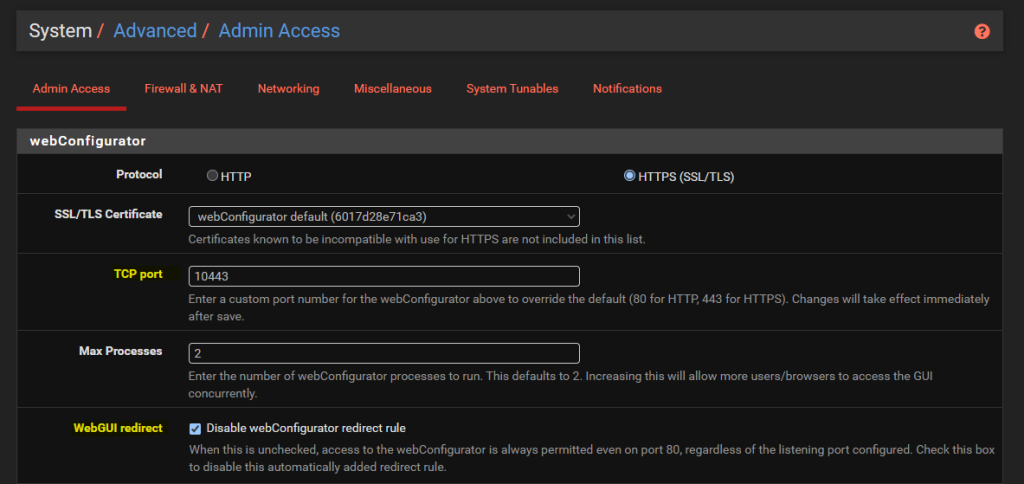
Configure pfSense System > Advanced > Admin Access
By default the pfSense WebGUI runs over port 80 and 443. What this means is that if you want to host a website behind pfSense then you need to re-configure this since your websites are going to be running over either HTTP or HTTPS.
To do this, simply change the TCP Port to an available port and disable the webConfigurator Redirect Rule as can be seen below;
Install HA Proxy via pfSense Package Manager
The first place to get started is to install the latest version of HA Proxy via the pfSense package manager by navigating through to System > Package Manager > Available Packages. Simply install the package and you’ll see this software now available for you to manage and configure.

Whenever you install packages within pfSense you’ll notice different menu items start to appear where you can configure the package and/or view the current use of it. The core menu item for configuring HA Proxy is under Services > HA Proxy;

HA Proxy Terminology and Architecture
Before we jump into the configuration for how to setup HA Proxy to host multiple websites, it’s first important to make sure we understand the overall architecture and how things fit together as the terminology and user interface often isn’t as clear as it could be for someone brand new to this. By understanding this, the configuration we’re going to go through below should hopefully make much more sense why we are configuring the things we are and ultimately will help you work with HA Proxy better in the future.
The below architecture is what we’re going to talk through in this guide for how to setup HA proxy on pfSense to allow you to host multiple websites behind a single IP address using a shared front end;
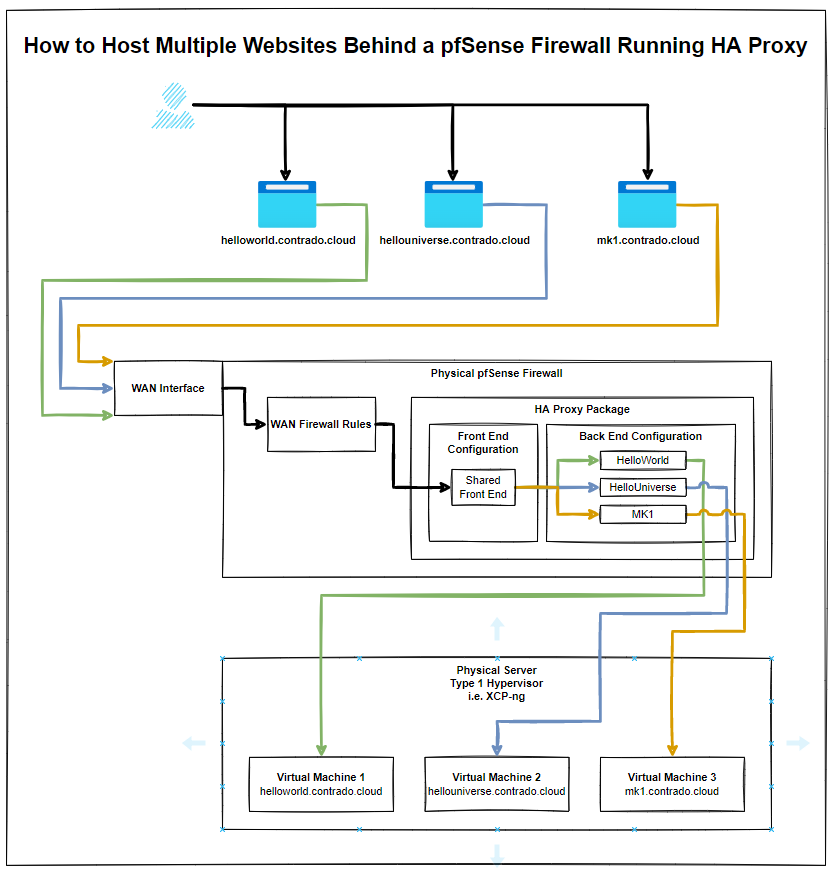
The core bits of terminology in HA Proxy that may not be as familiar to those coming from a web development background are the concepts of Front Ends and Back Ends, since these mean significantly different things in the world of web development. In web development, Front End generally refers to technologies such as HTML, CSS, JavaScript. And Back End tends to refer to server side technologies such as Java and C# to name a few for the purpose of illustration.
Those more familiar with scalable infrastructure in the web development world will be more used to the terms from cloud platforms such as AWS where there is the use of Application Load Balancers and Target Groups.
How this translates into HA Proxy terminology is that an Application Load Balancer in AWS terminology is essentially a HA Proxy Front End, and the AWS Target Group is equivalent to HA Proxy’s Back End. i.e. it is a configuration space that ultimately points to an upstream server somewhere.
And for those of you familiar with Nginx and using this as a reverse proxy, then the Back End in HA Proxy terminology tends to align closely with Upstream Server in Nginx terminology. All fun and games when every piece of technology calls essentially the same thing something completely different.
Anyhow, hopefully that’s helped to clarify a few bits of the terminology related to HA Proxy and how it loosely aligns with terminology that you may be more familiar with if you’re coming from a cloud native or web development background.
Configure HA Proxy Settings
So far all we’ve done is install the basic package with nothing configured and nothing turned on. Now we understand the architecture as explained earlier, it’s time to jump into some of the settings. First we’ll get started with the overall HA Proxy Settings.
Turn on HA Proxy
Firstly, let’s make sure HA Proxy is turned on;

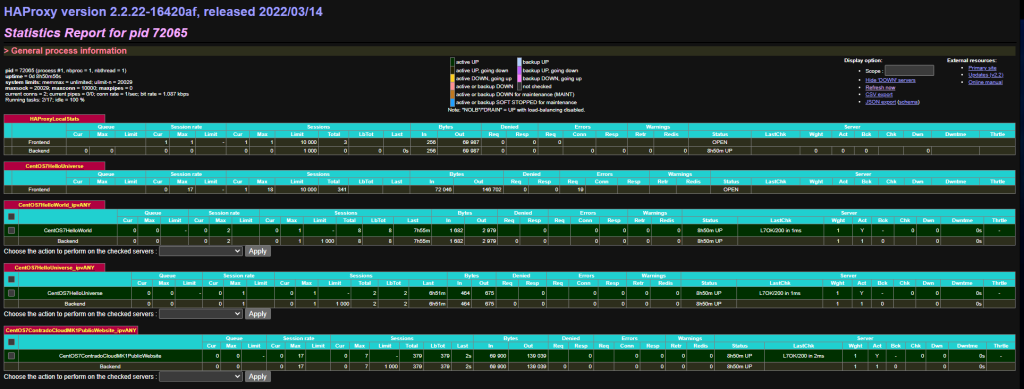
Turn on HA Proxy Statistics
To do this simply configure a relevant port on the settings page;

What this gives you is an extremely handy report that you can view from Status > HA Proxy Stats page which allows you to view lots of valuable information so you can understand how many sessions are hitting your Front Ends and Back Ends in HA Proxy once these have been set up a little later. This is significantly valuable when trying to debug things if they aren/aren’t working. Jumping ahead a little, but this is worth turning on while you are in this area of the configuration’
Configure the Max SSL Diffie-Hellman Size
Don’t ask me what this is, I genuinely don’t have a clue at this point in time of writing. An error message showed up in HA Proxy/pfSense when configuring future steps below which needed this setting up. So hey, do what it recommends – Seems odd that it wouldn’t automatically populate with best practice and requires a manual configuration but hey, probably one for a future contribution to the open source project by someone;

Summary of Settings Configuration
You’ll notice that we’ve skipped over a lot of the settings that are available to configure and for genuine reason. And that is that you just don’t need the majority of them to get a basic setup in place to start testing this stuff.
Sure, in a production environment you’re going to need to get finer tuning in place, but while you’re learning this then it’s more important to get a basic setup in place that you can play with and improve from there.
Setup Your Virtual Machines
Ok, so for the purpose of this blog post I’m going to assume you already have got some virtual machines set up and working in the way you want with the appropriate security in place to ensure that they are securely segmented for public access.
In our example, we’ve got the three virtual machines that are powering;
- contrado.cloud
- contrado.cloud
- contrado.cloud
In this example they have simply been configured to run Apache / httpd, configured to ensure httpd runs on startup, configured to allow inbound http traffic and added a basic index.html page in /var/www/html/index.html so that we can easily see which server we are on. Beyond that, everything else is out of the box on these virtual machines.
Configure HA Proxy Back Ends
This seems really counter intuitive to do this first, but it’s essential to do this first. This is what we’re going to achieve with this example;
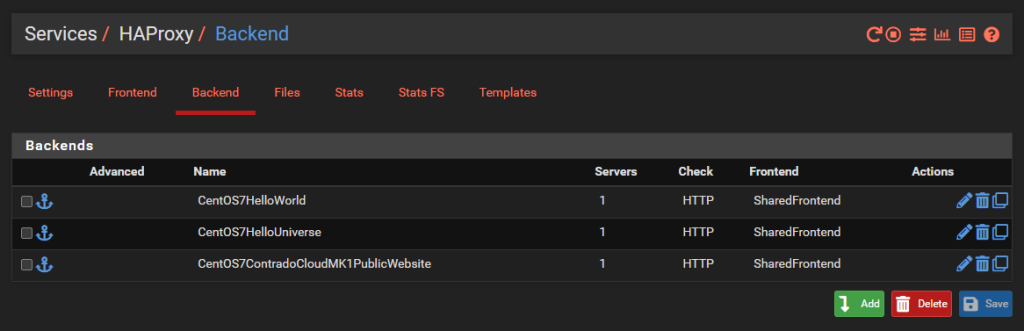
And we’ll dig into a single one as an example, the others are the same though with no differences beyond IP addresses. So configure your first Back End in HA Proxy;
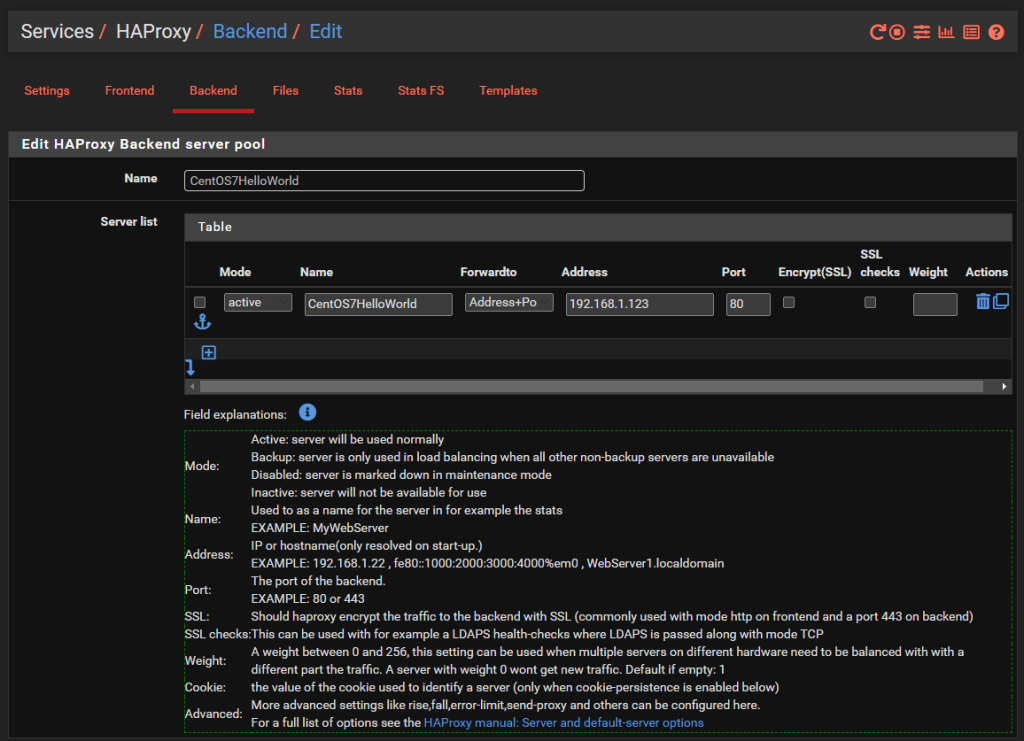
You’ll notice that the IP address is on the 192.168.1.0/24 LAN network which is clearly insecure, as is the Port 80 for insecure HTTP traffic for any real world production environment. But at least this gives an example for how to get this set up as a starting point.
There is nothing really to configure as a basic setup beyond the above. You can go configuring the Health Checking if you like, which is essential in production environments with High Availability Front Ends and disposable back end servers and infrastructure as code, but that’s well beyond the scope of this blog post. So either disable this by setting the option to None or configure as per your needs.
Rinse and repeat for your other virtual machines that you want to expose to the internet.
Configure HA Proxy Shared Front End
Note, if you are only hosting a single website then you can use a basic Front End rather than a shared front end, the configuration steps are very similar. You actually don’t even need to use HA Proxy if you are only hosting a single website as you can use basic Port Forwarding in pfSense as we’ve previously written a basic guide for on how to host a single website behind a pfSense firewall which you should check out if this situation applies to you.
Now that you have all of your Back End HA Proxy configured, it’s time to apply a Front End to handle traffic from the internet in a way that suits your needs. As this blog post is about hosting multiple websites behind pfSense using HA Proxy, the reality is that this is going to be primarily determined by the hostname of the incoming request, i.e. http://helloworld.contrado.cloud or http://hellouniverse.contrado.cloud or http://mk1.contrado.cloud etc.
For context, HA Proxy is really designed for traditional network infrastructure where you essentially don’t expose anything to the internet and anything you do you do minimally and with great caution. In the world of cloud and web development, well, this doesn’t quite meet expectations. There will be future blog posts about other supporting technologies in due course which significantly expand the capabilities and functionality that is explained in this blog post. This is just the basics for now.
What we’re aiming to achieve with a shared Front End in HA Proxy is the following;
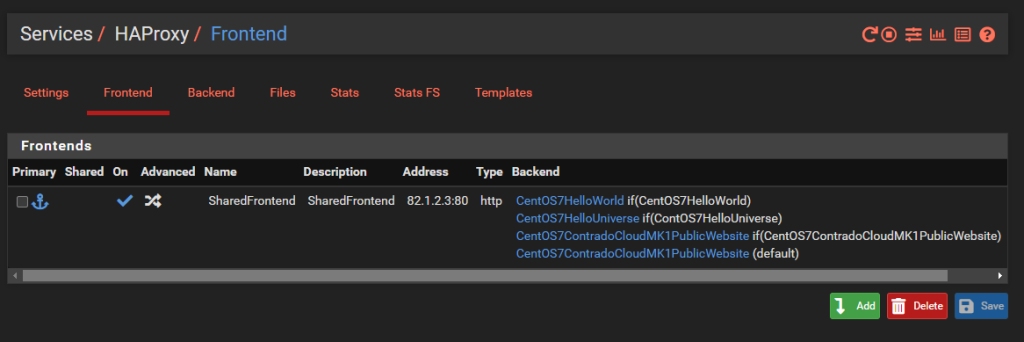
What you’ll notice is that this is purely for Port 80. This comes back to the point raised earlier that the default behaviour for pfSense and HA Proxy in general is to disable all and specifically permit inbound rules. In reality, any website that is being hosted is highly likely to require multiple ports to be opened to be managed remotely with ease such as HTTP, HTTPS, SSH, SFTP and many more. That all comes down to your specific use case though, so this blog post is simply designed to get you going in the right direction, not give you all the answers to your specific use case.
Jumping into the specific details of the above to get clarity on how this is configured. Simply give the Front End a Name, Description, make sure it’s Active and listening on the WAN on port 80 then set the Type to ‘http / https (offloading)’ as can be seen in the image below;
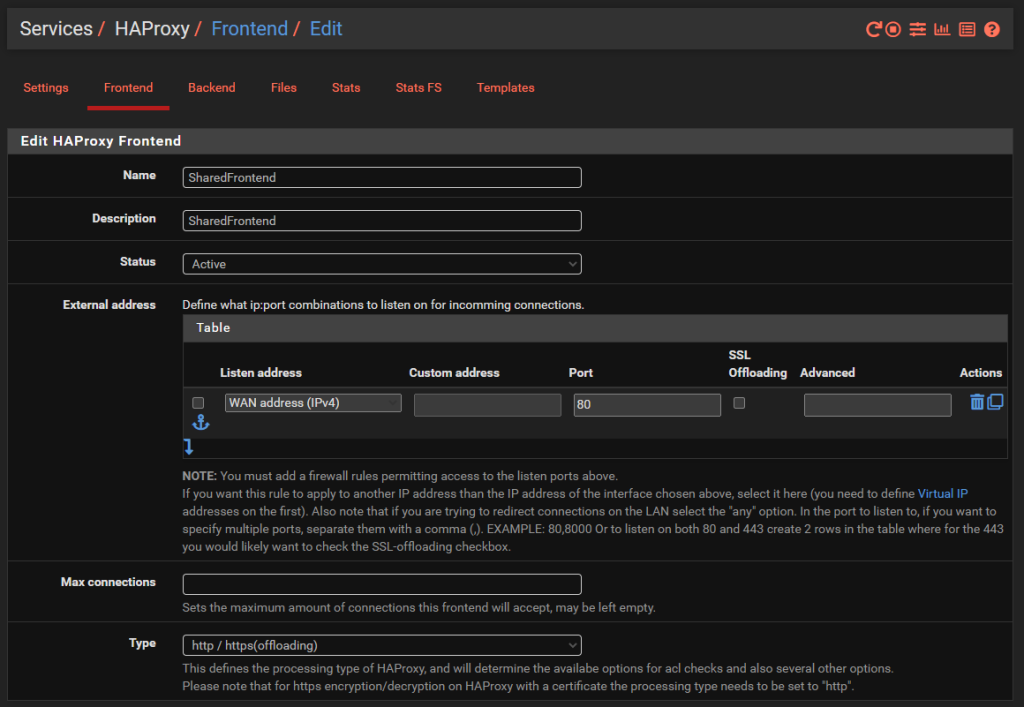
The next bit of configuration on your Front End is to configure what rules you need in place to allow your front end to talk to multiple back ends depending on your setup. For this blog post we’ve simply got the 3x virtual machines powering the HelloWorld, HelloUniverse and MK1 sub-domains to see how this works.
Firstly, configure your Access Control Lists which in this example simply gives you a way to map a hostname to a friendly name.
Next, configure the Actions by mapping how each of the Access Control List friendly names maps to a Back End in HA Proxy. The user interface in here isn’t the best if I’m honest. These things should be selectable dropdowns rather than free text field as it causes confusion, but hey.
Finally, select which is the default Back End so that HA Proxy knows where to send traffic when it doesn’t know what to do with it.
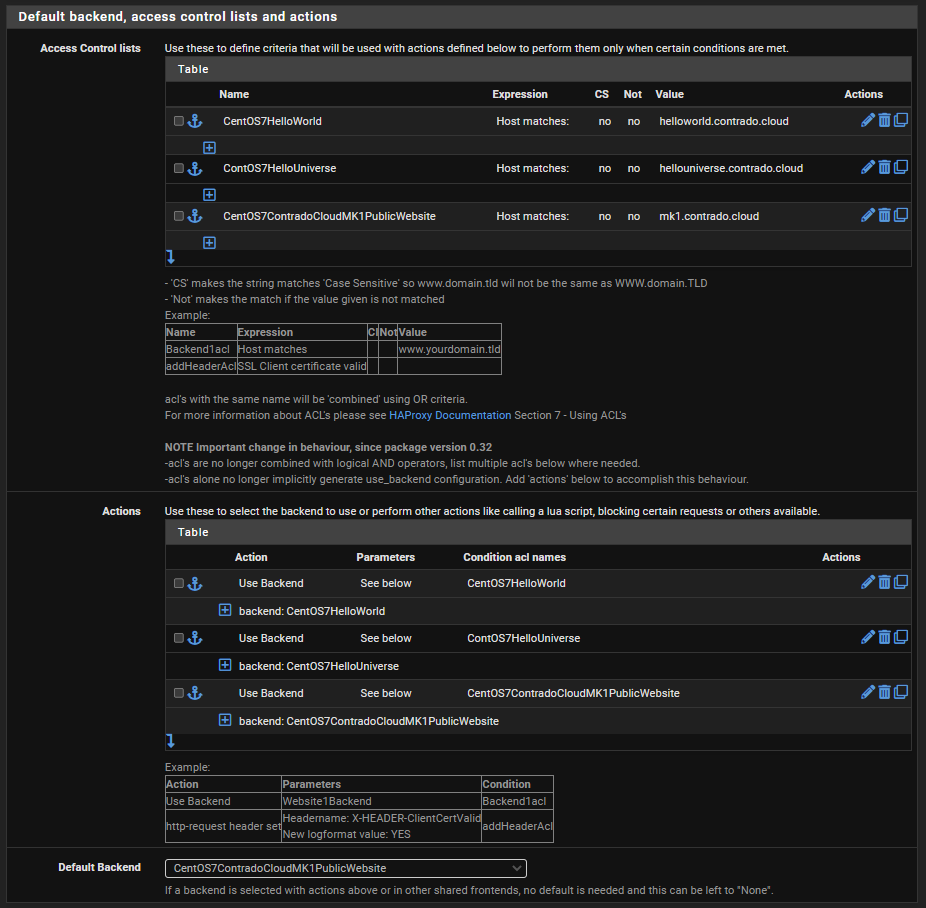
And that’s it for configuring HA Proxy. There are so many different settings throughout all those different screens we’ve looked at, but ultimately to get a very basic implementation set up so you can have a baseline to play with and improve up, this is all there is to it.
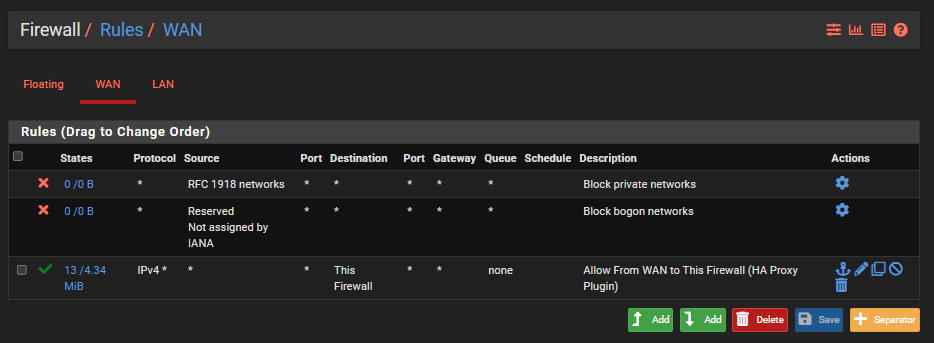
Configure pfSense Firewall Rules
Last step is to ensure you have a firewall rule on your WAN interface so that inbound traffic to the WAN from the internet can talk to the firewall and hence HA Proxy so that HA Proxy can then direct the inbound traffic to the correct destination based on what you have configured. Note that the top two rules in the screenshot below are out of the box pfSense rules to protect your network.
Check Everything is Working
Now simply navigate to your Sub-Domains and check everything is loading correctly as you expect.
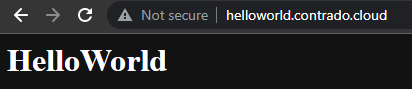
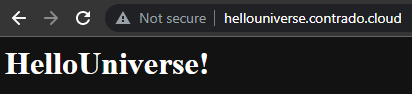
Awesome!
Final Considerations
This blog post is an extremely basic setup looking at only a single port. In reality, websites are complex, particularly when hosting a wide variety of services and even more complicated when you start to look at how SSL certificates are managed and where etc. Things start to get significantly more complex from this point.
Also, don’t forget to configure things such as static IP addresses for your virtual machines, ensure Apache or Nginx is starting on boot and your firewalls on your virtual machines are allowing inbound traffic on the ports you require open as most operating systems these days default to only allowing SSH traffic in by default.
There are a lot of jumps that your connection is going through as you work through the steps, so if something isn’t working for you, be extremely methodical to trace this through step by step and confirm if the traffic is hitting the next hop or not. This is often half the battle getting these things set up properly.
Summary
Hopefully by now, the pfSense and HA Proxy architecture diagram from earlier in this blog post is making sense what we’ve configured and how we’ve configured it. All of this should help get you going in the right direction to then further customise this to your specific use case.
As always, keep security in mind at all times. What has been outlined above is an extremely insecure setup on a flat network and running over HTTP. All of the IPs and custom configurations have naturally been changed for the purpose of this example tutorial as it is designed to get you understanding the basics. We’ve other blog posts on the site for how to configure things such as managed switches and pfSense so take a look around for other helpful content.
Hey, if you’re lucky and you test one of the hostnames that have been mentioned on this site, you may even see the websites up and running. The underlying infrastructure behind this is very much a part timer at the moment, only turned on when I’m having a play around.
by Michael Cropper | Aug 20, 2022 | Developer |
Ok, before start let’s acknowledge that this blog post is an extremely complex topic. That being said, let’s get the foundational understanding in place for the readers before we jump into the complexities.
What is Xen
Xen is simply the type 1 Hypervisor that runs on the bare metal, aka. Xen Project. This is an open source project that has had an enormous amount of contributions from the big players including Citrix, Arm, SuSE, AWS, Alibaba, CentOS, Debian, Oracle, RedHat, Ubuntu, XCP-ng and many more.
What is Citrix Xen Centre
Citrix Xen Centre is the software that is installed on a separate physical machine that is used to control Xen. Such as spinning up new virtual machines, configuring networks and managing storage.
What is XCP-ng Centre
XCP-ng Centre is the software that is installed on a separate physical machine that is used to control Xen. Such as spinning up new virtual machines, configuring networks and managing storage. This software is a fork of Citrix Xen Centre which was created during the transition to fully open source where Citrix released the reigns and control on the project.
What is Xen Orchestra (XO)
Xen Orchestra (XO) is the open source technology for managing Xen infrastructure via a user friendly web based user interface to allow the general user to control everything than Xen can do under the hood. Whereas Citrix Xen Centre and XCP-ng Centre are installed applications on a separate physical device, Xen Orchestra can be run within a host itself.
What is really interesting about Xen Orchestra is that you can actually install it within a virtual machine on a physical server where XCP-ng Server installed on. You may think this is counter intuitive and, well, it kind of is because from a hierarchical perspective, the virtual machine is effectively controlling the parent server for spinning up new virtual machines and more. This is pretty cool, but as always, keep security in mind and plan these things well if you are doing this.
If you’re looking for a guide on how to install Xen Orchestra (XO) from Sources then checkout the link. This guide will talk you through the finer details of how to get Xen Orchestra setup with ease to help you manage your virtual machines with ease and without limitations.
What is Xen Orchestra Appliance (XOA)
Xen Orchestra Appliance (XOA) is the commercial implementation of the open source Xen Orchestra (XO). This is managed by Vates, a French company who is leading the development of the open source project to maturity. Hat’s off to them and Olivier Lambert as the lead.
Architecture
So what does all this mean? Well, essentially that Xen / Xen Server / XCP-ng Server is installed on the physical machine and that this can be controlled / manged using either Citrix Xen Centre, XCP-ng Centre, Xen Orchestra (XO) or Xen Orchestra Appliance (XOA). Simple right?
Think of the control systems (Citrix Xen Centre, XCP-ng Centre, Xen Orchestra and Xen Orchestra Appliance) as input/control devices. In much the same way that a keyboard and mouse act, they are both input devices into a computer where you can achieve the same goals in one way or another.
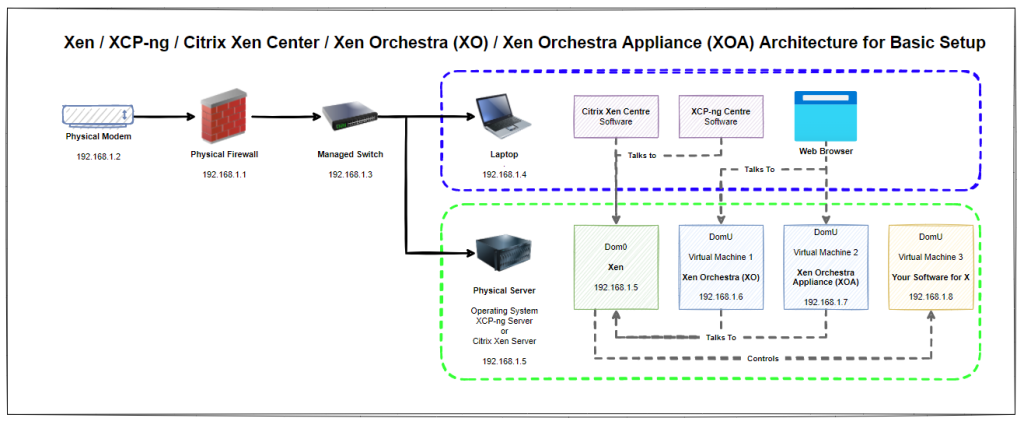
Naturally for this basic setup you’ll notice that everything is on a flat network, aka. no securely segmented networks. This is rarely a good idea in a production environment, but at least this basic setup helps you to get the base level understanding for how things plug together under the hood and helps to align terminology and understanding.
What is not always commonly understood is that Citrix Xen Centre can control both Citrix Xen Server and XCP-ng Server. Likewise, XCP-ng Centre can control both Citrix Xen Server and XCP-ng Server as XCP-ng was forked from the Citrix setup when it was open sourced. Quite handy to know.
Synchronisation
What is important to understand with all the above in mind is that it is not the tool that is mastering the configuration data, but the tools are there to control the mastering of the configuration data. What this means is that if you have multiple of the control devices installed on your machine then you’ll notice that they all update whenever one of them updates the configuration, as they are all reading/controlling the same physical device.
Summary
Given the above descriptions and architectural diagrams, hopefully it is now clear how you can manage Xen using a multitude of tools based on your individual user preference. What is hopefully clear is that this is a complex topic and one that often ends in a question being answered as “it depends”.
Hopefully this blog post has helped to align understanding of how the different dots connect together to help you in your understanding of what you need to achieve for your specific use case.
by Michael Cropper | Aug 15, 2022 | Developer |
To ensure terminology is fully understood, XOA stands for Xen-Orchestra Appliance. It is the commercial side of Xen-Orchestra, which to add to confusion, also offers a free version of XOA with a slightly limited feature set.
So when we say “Install XO from Sources” what this actually means is that we’re installing the open source Xen-Orchestra, not the commercial XOA aka. Xen-Orchestra Appliance.
One important point that many people don’t realise is that Xen-Orchestra can actually manage the physical host server where it is installed within a virtual machine on that server. Pretty cool, right.
Step 1 – Create a Virtual Machine Running Debian 11 Bullseye
Firstly, give this virtual machine as much vCPUs and RAM that you can spare on the initial setup as this is a fairly resource intensive task getting this setup. Thankfully there is a handy XenOrchestraInstallerUpdater piece of software on GitHub from Roni Väyrynen and other contributors.
I’ve chosen the above as at the time of writing Debian 11 Bullseye is the latest supported Debian version that the above script supports.
Step 2 – Understand Sudo Permissions Have Changed in Debian 10 + 11
Yup. Your usual ‘sudo –s’ command and SSH’ing in as a root user simply no longer work on Debian 10 + 11. A rather annoying undocumented piece of information given the significance of this change. But hey, that’s why I’m writing about it here.
By default on Debian 10 and Debian 11, the root user is not included in the sudoers list, so you can’t SSH in using the user ‘root’. And on top of that, if you try to SSH into your Debian 10 or 11 virtual machine as ‘{YourUsername}’ that you configured on setup, you’ll notice that if you run the common command ‘sudo –s’ to switch to the root user, you get an error saying that your username isn’t in the sudoers list.
Say what?
Anyhow, the new command seems to be “su –“ which behaves in the same way and gets you to where you need to be.
Step 3 – Install Git
We’re going to be pulling in and running the code from the GitHub repository mentioned earlier, so to do this we need to ensure Git is install on the virtual machine so that it’s possible to download the code we need for XenOrchestraInstallerUpdater.
Simply run the command;
apt-get install git
Step 4 – Clone XenOrchestraInstallerUpdater Git Repository
Next step is to get the code from GitHub down onto your virtual machine. So simply run the command;
git clone https://github.com/ronivay/XenOrchestraInstallerUpdater.git
This will download the code to the directory you are currently in. Make a note of this and make sure you’ve put this in a sensible place that you’re going to be able to find later on.
(Optional) Create a Self-Signed SSL Certificate
The reason why this step is optional is that for playing around you don’t really need to bother with this. But obviously for production environments you want to keep security at the forefront of your mind. To be clear, this isn’t a recommendation for how to use HTTPS in a production environment, this is simply a quick way of getting SSL up and running should you choose to experiment with this;
cd /etc/ssl
mkdir xo
cd xo
openssl req –newkey rsa:4096 –x509 –sha256 –days 3650 –nodes –out xo.crt –keyout xo.key
Step 5 – Create a Copy of Configuration Files
Thankfully Xen-Orchestra comes with some handy configuration files so you don’t need to start from scratch. To copy these and make them your own simply run the following command;
cp sample.xo-install.cfg xo-install.cfg
This is the copy command, aka ‘cp’. This is saying copy the file ‘sample.xo-install.cfg’ and then paste the file with a new filename to ‘xo-install.cfg’. The joys of Linux commands.
(Optional) Configure your Xen-Orchestra Configuration File
To do this, simply run the command;
nano xo-install.cfg
Now, you only need to do this if you’ve implemented the optional step above to create an SSL certificate. If you have done this, you need to specify the location of those certificate files within your Xen-Orchestra configuration file. As an example following on from the above, this is how your configuration file would look;
# Location of pem certificate/key files. Installation will automatically configure HTTPS if these are defined. Remember to change PORT variable as well.
PATH_TO_HTTPS_CERT=/etc/ssl/xo/xo.crt
PATH_TO_HTTPS_KEY=/etc/ssl/xo/xo.key
Save the file and exit.
Step 6 – Install Xen-Orchestra (XO) from Sources
Simply run the following command and watch as things progress;
./xo-install.sh
Wait a while, watch things progress and then you’re good to go.
Step 7 – Confirm Setup Works
You’ll know that the setup works for two reasons. Firstly, the console will have lots of success messages and will tell you that everything has completed successfully. Secondly, you’ll now be able to access the IP address of the virtual machine in your web browser to login to Xen-Orchestra, the completely free and unlimited feature access to the platform so you can play around to your hearts content. Job done.
The default username and password for XO Xen-Orchestra is;
Username: admin@admin.net
Password: password
Naturally I don’t need to remind you that this is extremely insecure, so make sure to change this once you’ve got this setup.
Summary
So that’s how to get XO aka. Xen-Orchestra set up on a virtual machine inside a physical XCP-ng Server so that you can have a play around. You’ll notice that this is slightly different than how to get XOA setup via the Quick Deploy feature once you’ve got XCP-ng Server setup, but that’s a fairly straight forward click and configuration setup, but with limited features at the end of it.
The above shows you how to get the basics set up in no time with relative ease and one core dependency on the script from GitHub. The contents of this blog post have been pulled together from various snippets of insight around the internet to provide a clear guide for how to do this, with a couple of key mentions being LTS and Vates and Roni Väyrynen for both help with online video content and conversations to help identify the nuggets of information joining the dots together with the information for how to get the above setup with ease, at least the missing nuggets of information in my brain – it may be straight forward to others!
by Michael Cropper | Aug 9, 2022 | Developer |
This is quite a complex topic, and one that all depends on your specific setup. So we’re going to take a look at some of the options for how to get this set up with ease. Is what we’re going to talk through the best practice? Not sure. But I’ve not found any useful information online for a better approach, so to quote Admiral Adama from Battlestar Galactica when asked the question “So what’s your plan here?” he answers “Personally, I tend to go with what you know. ‘Til something better turns up”. So if the readers of this blog post have any better ways of doing this, please do share in the comments.
Physical Network Hardware
So let’s get some basics documented. The reality is that every single physical network hardware is going to be different for every organisation. But fundamentally and at the most basic level everyone has at a minimum: Modem –> Firewall –> Managed Switch –> XCP-NG Server –> Virtual Machine(s)
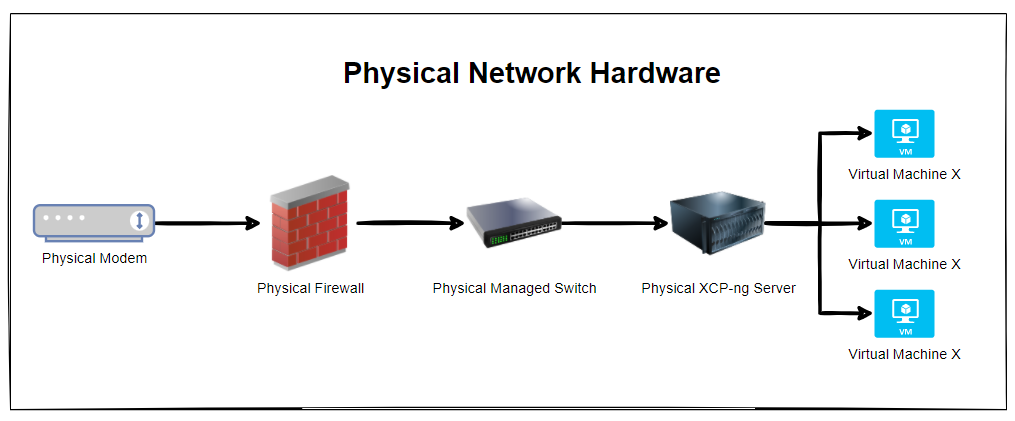
The reality is that in most home setups when people are getting started, most people start off with a single device supplied by the ISP (Internet Service Provider). Often these devices act as everything and nothing, so they perform the absolute basic requirements of a modem, a firewall and a switch, but fail on most things as they can’t handle VLANS, they can’t handle complex firewall rules and they can’t effectively manage complex networks. Typical jack of all trades, master of none.
Ultimately if you are in this home lab setup and wondering why things don’t work. It’s highly likely because you simply don’t have the physical hardware that you need to achieve what you want. Consumer grade hardware simply doesn’t cut it, even the high end consumer grade hardware as this is often designed to visually look powerful through curves/edges and more antennas in design rather than actually being powerful under the hood. Unfortunately in the UK we don’t particularly have the equivalent of an ecommerce store for this kind of stuff to make life easy, the way things work is often behind complex business to business commercial relationships and ‘special’ pricing etc. It’s an absolute nightmare. Perhaps I need to get around to building a business model to help to simplify the supply chain for these things, when I get the time. But hey, I digress. Back to the topic at hand.
Now things get a little more complex than the above as there are physical cables that are connecting the different physical devices, so let’s expand the above architectural diagram to understand the next level of detail. Here we have the setup whereby the firewall has 3x physical ports on the device and we have configured the firewall to have a simple setup of one port = one VLAN.
In reality, many VLANs often share a single physical port on the physical device, but let’s leave that for another blog post to cover off. So then we have the managed switch with the basic setup of 3x inbound connections and 3x outbound connections, each matching a one to one relationship to keep things simple. Again, the reality of any real world implementation is that we use things called Trunk Ports which is just a term that means a physical port that allows traffic to flow to the next physical device for every VLAN and untagged (aka. non-VLAN traffic).
What this ultimately leaves us with is the setup as follows;
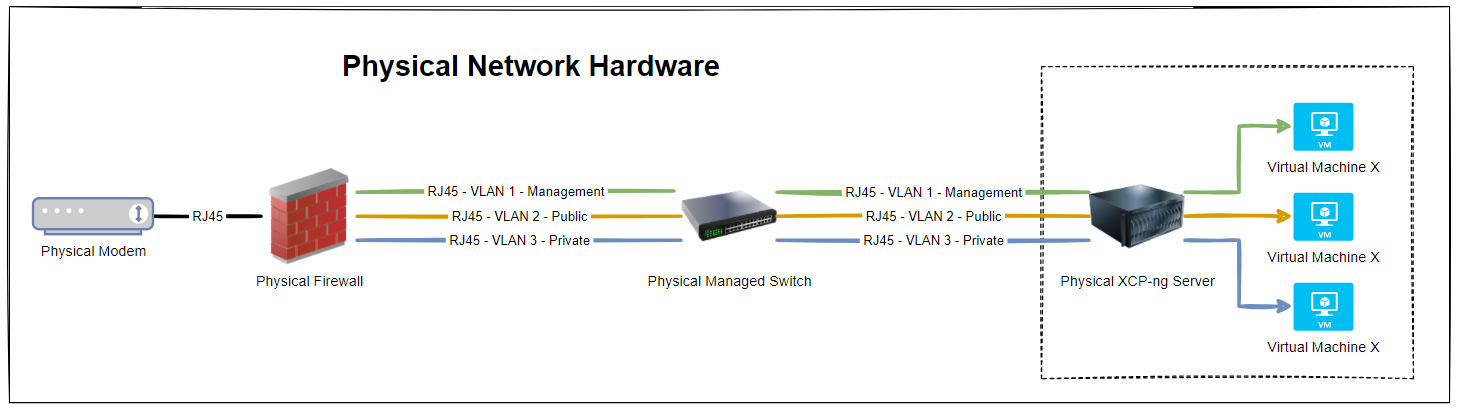
So we have 3x physical RJ45 cables connected between the physical firewall and the physical managed switch, and then another 3x physical RJ45 cables connected between the physical managed switch and the physical type-1 bare metal hypervisor XCP-ng Server. Everyone’s setup is going to be different, but if you’re working with Ubiquiti/UniFi then this guide on how to setup a UniFi managed switch is going to be handy.
But, we’ve jumped ahead a little. You’ll notice in the above diagram that the virtual machines are magically attached to the correct VLANS. But how? You may ask.
How to Configure XCP-ng Centre Networks on First Setup
When you first get XCP-ng Server setup and XCP-ng Centre setup, you’ll notice that when you plug in all the Ethernet cables that you are simply presented with a bunch of un-identified networks that you need to figure out what to do with;
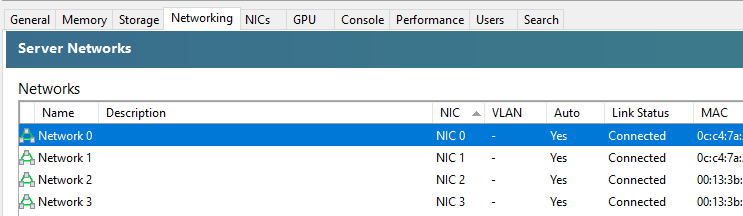
The networks that are listed here within XCP-ng Centre are directly related to the physical ports that you have available on your XCP-ng Server. So you’re probably thinking, awesome, let’s get started and get a virtual machine spun up and get cracking. But it’s not so straight forward. How do you know which network to attach the virtual machine to? After all, your choice here can have security implications depending on your use case. You don’t want a publicly accessible virtual machine to have access to your management network.
So we need to get into the topic of how to identify what networks in XCP-ng Centre map to what VLANs so that you can label them correctly and ultimately use them properly within your configuration. As with everything important, naming conventions and terminology is extremely important so make sure you agree this within your own organisations as appropriately.
The best way I’ve found to easily get this mapped in the first instance is actually quite simple, while not obvious, and it also feels quite rudimentary, it does work. Simply create multiple virtual machines, each one dedicated to a single network, then see what IP address it gets assigned from your DHCP server (likely managed on your firewall and enforced through VLAN configuration in the firewall and managed switch).
This is assuming you’ve already got your XCP-ng Centre configured to connect to your ISO Storage Repository for loading operating systems.
This step certainly feels a bit like using a sledgehammer to crack a nut, but it works. But I’ve yet to find a simpler way to achieve this. Once you’ve gone through this process and run the equivalent of “what’s my IP” (aka. ipconfig or ifconfig etc.) on the virtual machines once you’ve set them up and SSH’d into them, you’ll know definitively which network they are configured against.
So now you need to rename your networks within XCP-ng Centre.
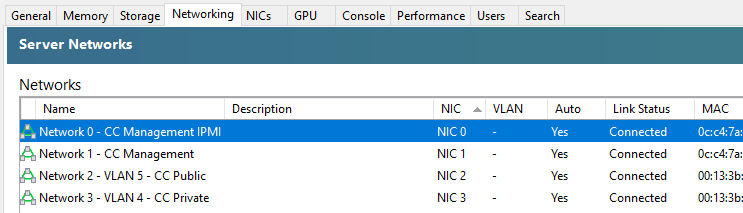
You’ll notice in the above screenshot that we don’t have the VLAN column populated, and that is purely because there are pending internal decisions to be made around the above setup on this specific use case, but you get the idea of how you can make sure the Network Interface Cards (NICs) map through to the XCP-ng Centre networks.
As with everything in IT “It depends” 😀
Summary
The reality is that what we have gone through in this blog post is an extremely basic setup in the real world. What I hope has been conveyed throughout this blog post is one practical way of mapping when things are physically plugged-in to different network ports and how we can determine which actual networks they belong to before we start deploying different virtual machines for different use cases.
by Michael Cropper | Aug 7, 2022 | Developer |
Ok, so we’ve done a recent blog post on how to setup XCP-NG Tools on CentOS 7. So this blog post is going to be a rather similar blog post which a few nuances.
Pre-Check
You’ll notice that XCP-NG Tools is not installed when you check the Performance tab against your Debian 11 Bullseye virtual machine as you’ll see the message “To view memory data for this VM, you need to install XCP-ng VM Tools”;
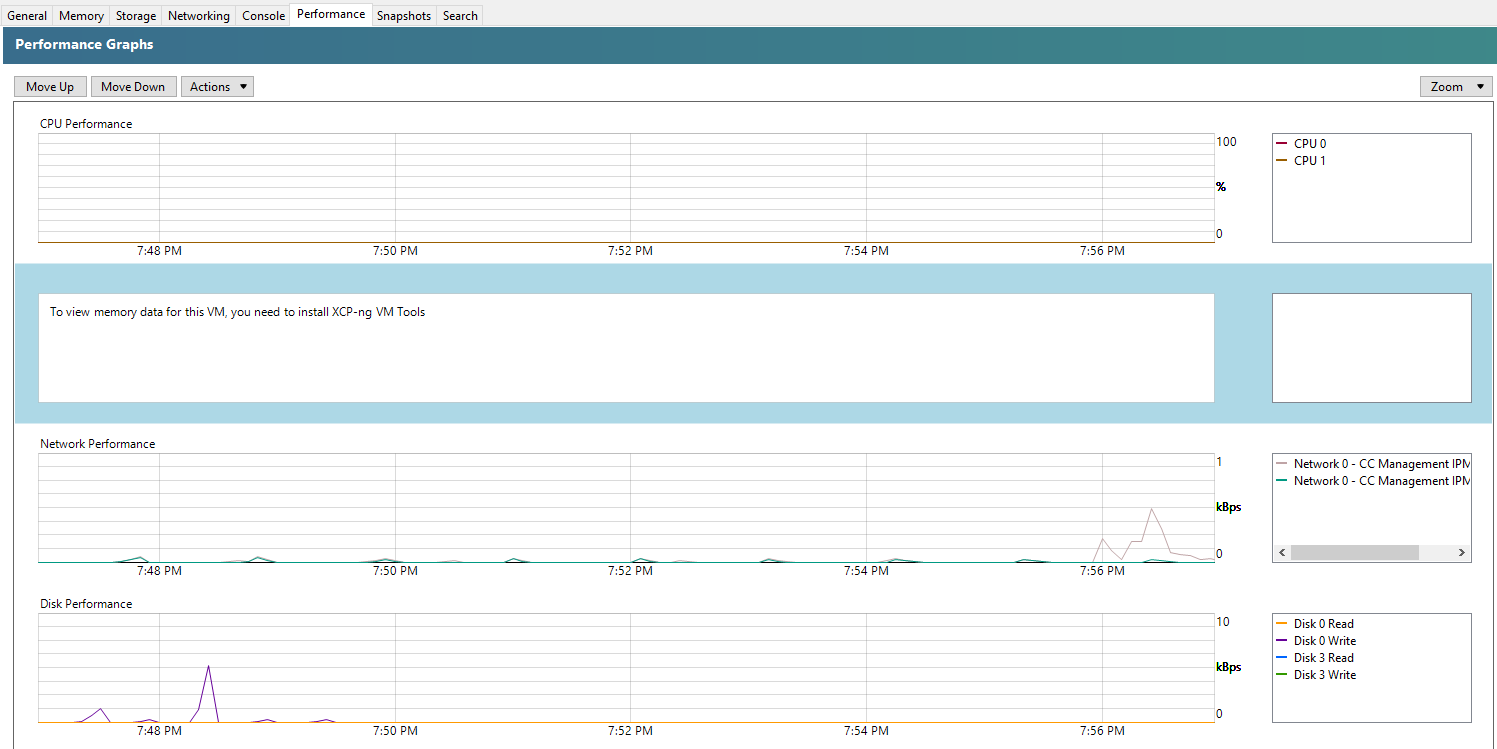
Step 1 – Insert the guest-tools.iso in the Virtual Disk
To do this, go into your virtual machine within XCP-NG Centre, then into the Storage tab, then make sure that within your DVD Drive you have the XCP-NG VM Tools is selected;

Step 2 – SSH Into the Virtual Machine
Next step is pretty straight forward, SSH into your virtual machine so you can run the commands to install XCP-NG Tools on Debian 11 Bullseye.
Step 3 – Switch to Sudo
This step is one that isn’t particularly well documented online. As of Debian 10 Buster release and also continued within Debian 11 Bullseye release, to switch to the sudo user you need to run the command;
sudo –

Step 4 – Mount the CD-ROM/DVD Drive
This step is to ensure that your Debian 11 Bullseye can access the contents of the virtual CD-ROM/DVD Drive that we configured within step 1. To do this, simply run the command;
mount /dev/cdrom /mnt/
What the above command is saying is…..Mount the folder path at /dev/cdrom to the folder location /mnt/ – There is nothing more to it than that.
Step 5 – Run the install script for XCP-NG Tools
Now that your Debian 11 Bullseye virtual machine has access to the contents in your virtual CD-ROM/DVD Drive which contains the guest-tools.iso contents, it’s time to run the installation script.
bash /mnt/Linux/install.sh
Follow the steps and you’re on your way. You’ll know that XCP-NG Tools has been successfully installed because you’ll get a confirmation message;
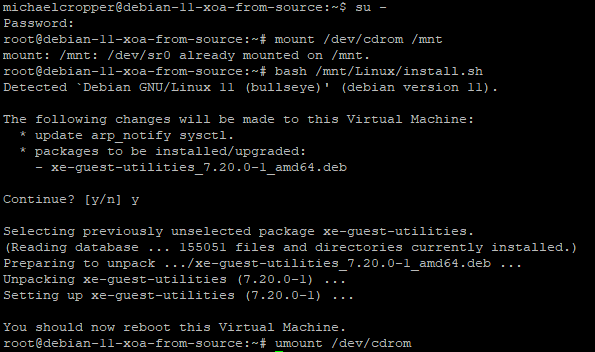
And you’ll also note that within the Performance tab against your Debian 11 Bullseye virtual machine that the memory data starts to come through in a matter of minutes at the absolute most, in most cases in about 30 seconds, even without rebooting;
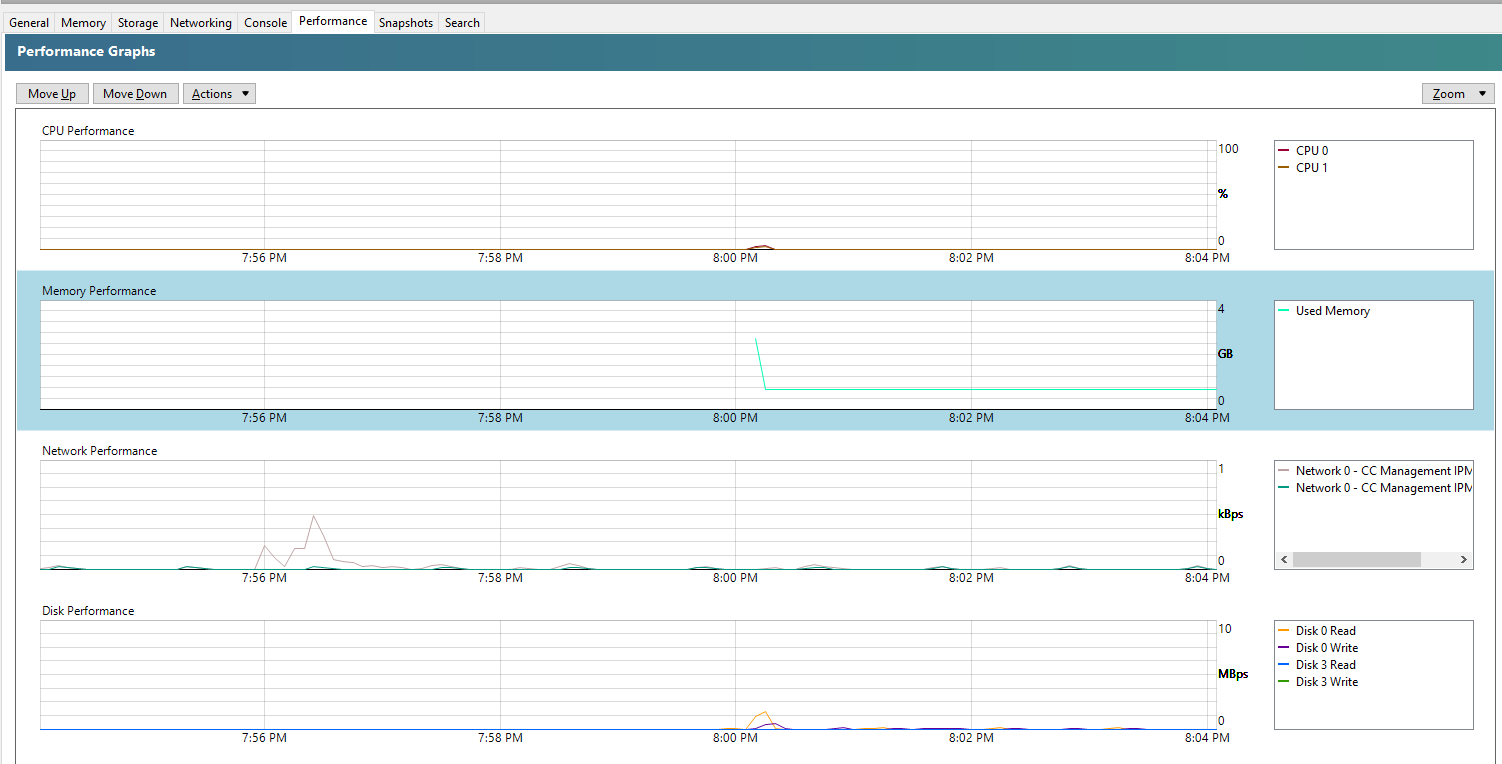
Summary
When you follow these simple steps, it’s a few clicks and commands to get XCP-NG Tools up and running on Debian 11 Bullseye via XCP-NG Centre. For every virtual machine that you setup, make sure you install XCP-NG Tools to make your life as easy as possible.

































